samvartaka

• Home
• About
• Publications
• Archive
• Tags

VolgaCTF 2016 Quals - Five Blocks (Crypto 600) Writeup

• crypto 9
• ctf 1
• differential cryptanalysis 1
• meet-in-the-middle 1
• feal4 1
• lai-massey 1

This year’s VolgaCTF Qualifications featured a very interesting crypto challenge which involved some block cipher cryptanalysis, something rarely seen in Capture The Flag (CTF) competitions. While the cryptanalysis in question obviously concerned older or reduced ciphers, interesting practice in this area can be hard to come by. And while cryptanalysis of this kind isn’t going to break any modern, decently designed and reviewed, cipher there is plenty of proprietary cryptography out there, especially in the world of embedded and constrainted devices as shown by eg. the work of Verdult et al. on physical access control systems, vehicle immobilizers, etc. and the work of Meijer et al. in breaking the crypto employed by hardened Mifare Classic cards.

There isn’t a whole lot of comprehensive entry-level material on cryptanalysis out there mainly because, as Bruce Schneier said, “cryptanalysis is such a fast-moving field that any book of techniques would be obsolete before it was printed. And even if the book could somehow remain current, it would do little to teach cryptanalysis. The only way to learn cryptanalysis is through practice”. Still, some material is easier to digest than others and most cryptanalytic papers are usually not among the former. Some good resources on cryptanalytic fundamentals and basic techniques are Roel Verdult’s “Introduction to Cryptanalysis: Attacking Stream Ciphers”, Jon King’s website and his talk at LayerOne 2013, Kerry McKay’s “Understanding Cryptology: Cryptanalysis”, Howard Heys’ tutorial on linear and differential cryptanalysis, Bruce Schneier’s “Self-study course in block-cipher cryptanalysis”, Eli Biham and Adi Shamir’s tutorial, Christopher Swenson’s book “Modern Cryptanalysis” and “Applied Cryptanalysis” by Mark Stamp and Richard Low.

As it turns out, the CTF team h4x0rpsch0rr (the only team to solve the challenge during the CTF) published a writeup of this challenge right as i was writing mine so there’s some overlap there but i hope this post still helps a bit in understanding the issues involved in differential cryptanalysis and meet-in-the-middle attacks. The accompanying code to this writeup is written in Python for understandability and not optimized for performance at all but should still finish within a ‘CTF-reasonable’ timeframe on a modern PC.

Challenge Description

The challenge description gave us a service address, some files to download and some hints:

It seems that this service merely encrypts the data we're sending to it. We managed to find a possibly valuable piece of encrypted data along with the server's script. Could you take a look and see if anything can be done?

nc five-blocks.2016.volgactf.ru 8888

server ciphers data

Hints

What would you get if you'd encrypted four-block data of the form AABC, where A, B, C are 64-bit arbitrary blocks?

Are the rounds of the second block cipher completely dependent or independent of each other? Or is the truth somewhere in the middle?

The data we can download is named flag.enc and probably contains the target flag encrypted with some unknown key. The server code looks like this:

            if not self.do_challenge():
                raise Exception('Failed to pass the test')
            with open(keys_file, 'rb') as f:
                data = f.read()
                key_bc1 = data[:6*4]
                key_bc2 = data[6*4:]
            cryptor = bcs(key_bc1, key_bc2)
            data_to_encrypt = read_message(self.request)
            iv = os.urandom(8)
            encrypted_data = cryptor.encrypt(data_to_encrypt, iv)
            to_send = iv + encrypted_data
            send_message(self.request, to_send)

The do_challenge routine is a proof-of-work routine to prevent bruteforce-like attacks. What we have here is an encryption oracle, we can supply any plaintext message and receive the corresponding ciphertext encrypted using the same static keys key_bc1 and key_bc2 which are drawn from the keys_file. So our attack scenario is a chosen plaintext attack. Let’s take a look at the cipher code:

class bcs(object):

    def __init__(self, key_bc1, key_bc2):
        self.bc1 = bc1(key_bc1)
        self.bc2 = bc2(key_bc2)

    def encrypt(self, data, iv):
        ciphertext = ''
        data = pad(data)
        C = iv
        for i in xrange(0, len(data), 8):
            A1 = self.bc1.encrypt_block(array.array('B', data[i:i+8]))
            A2 = self.bc2.decrypt_block(A1)
            ciphertext += block_xor(A2, C)
            C = A1
        return ciphertext

    def decrypt(self, data, iv):
        plaintext = ''
        C = iv
        for i in xrange(0, len(data), 8):
            A2 = block_xor(data[i:i+8], C)
            A1 = self.bc2.encrypt_block(A2)
            plaintext += self.bc1.decrypt_block(array.array('B', A1))
            C = A1
        return unpad(plaintext)

We can see the mysterious bcs cipher creates two seperate encryption objects bc1 and bc2 with the two keys supplied to it. We also see that input data is padded to a multiple of the blocksize (64 bits in this case) and that it employs a block cipher mode of operation that looks a bit like CBC mode but isn’t, the prime difference being that this mode of operation XORs the intermediate ciphertext with the IV rather than the intermediate plaintext. This image illustrates the construction:

It looks like we’re faced with a block cipher constructed out of two seperate block ciphers (one used in encryption direction, the other in decryption direction) so the best way to go about this is probably to attack both block ciphers seperately, recover their corresponding round keys and use those to decrypt our flag.

Chopping up the mode of operation

Since we have a chosen plaintext scenario it’s probably a good idea to extend this (as much as possible) from the general cipher to the individual underlying block ciphers, ie. we want to extract the following from our (plaintext, ciphertext) pairs:

• (plaintext_block[i], A1[i]) where A1[i] = bc1.encrypt_block(plaintext_block[i])
• (A1[i], A2[i]) where A2[i] = self.bc2.decrypt_block(A1[i])

We can do so as follows, consider a plaintext consisting of the following arbitrary 64-bit blocks: [A][A][B][C]. The corresponding ciphertext would look like:

[(D2(E1(A)) ^ iv)] [D2(E1(A)) ^ E1(A)] [D2(E1(B)) ^ E1(A)] [D2(E1(C)) ^ E1(B)]

So in order to extract E1(A) from this we take ciphertext_block[0] ^ iv ^ ciphertext_block[1] = (D2(E1(A)) ^ iv) ^ iv ^ D2(E1(A)) ^ E1(A) = E1(A). Now that we know E1(A) we can extract D2(E1(A)) as ciphertext_block[0] ^ iv so we have a chosen plaintext/ciphertext pair for the first blockcipher and a known plaintext/ciphertext pair for the second blockcipher. Note that once we crack the first blockcipher we can turn the known plaintext scenario for the second cipher into a chosen plaintext scenario by setting plaintext_block[0] = D1(chosen_plaintext).

Attacking the first block cipher: Differential cryptanalysis against modified FEAL-4

The next step is taking a look at the first block cipher:

def rot(x):
    return ((x<<4) | (x>>4)) & 0xff

def g_box(a, b, mode):
    return rot((a + b + mode) & 0xff)

def f_box(x):
    t0 = (x[2] ^ x[3])
    y1 = g_box(x[0] ^ x[1], t0, 1)
    y0 = g_box(x[0], y1, 0)
    y2 = g_box(y1, t0, 0)
    y3 = g_box(y2, x[3], 1)
    return array.array('B', [y0, y1, y2, y3])


class bc1(object):

    def __init__(self, key_data):
        assert (len(key_data) == 6*4)
        self.subkeys = []
        for i in xrange(0, 6*4, 4):
            self.subkeys.append(array.array('B', key_data[i:i+4]))

    def encrypt_block(self, plaintext):
        plaintext = array.array('B', plaintext)
        pleft = plaintext[0:4]
        pright = plaintext[4:]

        left = list_xor(pleft, self.subkeys[4])
        right = list_xor(pright, self.subkeys[5])
        R2L = list_xor(left, right)
        R2R = list_xor(left, f_box(list_xor(R2L, self.subkeys[0])))
        R3L = R2R
        R3R = list_xor(R2L, f_box(list_xor(R2R, self.subkeys[1])))
        R4L = R3R
        R4R = list_xor(R3L, f_box(list_xor(R3R, self.subkeys[2])))

        cipherLeft = list_xor(R4L, f_box(list_xor(R4R, self.subkeys[3])))
        cipherRight = list_xor(cipherLeft, R4R)
        return ''.join(map(chr, cipherLeft + cipherRight))

    def decrypt_block(self, ciphertext):
        ciphertext = array.array('B', ciphertext)
        cipherLeft = ciphertext[0:4]
        cipherRight = ciphertext[4:]

        R4R = list_xor(cipherLeft,cipherRight)
        R4L = list_xor(cipherLeft, f_box(list_xor(R4R, self.subkeys[3])))
        R3R = R4L
        R3L = list_xor(R4R, f_box(list_xor(R3R, self.subkeys[2])))
        R2R = R3L
        R2L = list_xor(R3R, f_box(list_xor(R2R, self.subkeys[1])))
        left = list_xor(R2R, f_box(list_xor(R2L, self.subkeys[0])))
        right = list_xor(left, R2L)

        pleft = list_xor(left, self.subkeys[4])
        pright = list_xor(right, self.subkeys[5])
        return ''.join(map(chr, pleft + pright))

The typical left-right alternations indicate we are dealing with a balanced feistel cipher of 4 rounds and the ‘f-box’ and ‘g-box’ terminology hints at the notoriously weak FEAL cipher. A modified version of FEAL-4 had featured previously in a CTF and a quick comparison with the FEAL-4 reference code confirmed this.

The difference between regular FEAL-4 and this version lies in the rotation function used as part of FEAL’s g-box, the original being:

return ((x<<2) | (x>>6)) & 0xff

and ours being:

return ((x<<4) | (x>>4)) & 0xff

Keep this in mind as it will be important later on.

There are multiple ways to break FEAL-4 (which makes it a good practice cipher for block cipher cryptanalysis) but i chose to go for the differential cryptanalysis attack as described by Jon King as differential cryptanalysis is well suited to a chosen plaintext attack. King’s tutorial is a great introduction to differential cryptanalysis but the reason why it’s so portable to both this challenge and the challenge from the CSAW 2014 quals is because in both cases FEAL-4 was used and the flaw that led to FEAL-4’s particular susceptibility to differential cryptanalysis (the 1.0 probability differential characteristic in the g-box modular addition design) remained unchanged, while what changed was the value of the output differential as a result of the changed rotation function. If the challenge designers had modified the g-box design further (or used a different block cipher susceptible to an attack of similar complexity) a deeper understanding of the process involved would be of much use. So with that in mind i thought walking through the process and pointing out where this attack process differs from King’s would be of some value.

Differential Cryptanalysis Basics

Without going too much in-depth i will outline some basics of differential cryptanalysis as it applies to FEAL-4 here (based upon King’s explanation but with extra details, particularly if relevant to the challenge). Note that we will have to start off with some basic explaining on differential characteristics before we can explain how they help us obtain round keys.

A lot of cryptanalytic attacks on symmetric ciphers involve a principle known as divide-and-conquer where we partition the cipher state into isolated parts which we can attack by themselves, for example by splitting up an iterated block cipher into its constituent round functions. The expected attack complexity cipher should be 2**64 (as that is it’s key size) in a brute-force attack but if we can attack each round seperately and recover the target round keys one by one, the attack complexity becomes 2**32 + 2**32 + .. + 2**32 < 2**64. See for example the following image taken from Verdult’s Streamcipher Cryptanalysis introduction

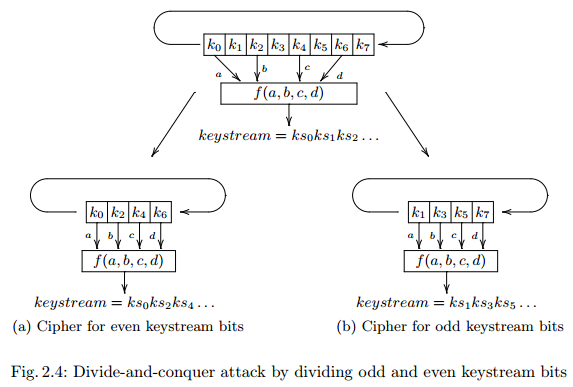
A good block-cipher structure (using proper diffusion) is designed to ensure that we can know at most the initial and final state (ie. plaintext and ciphertext) but not the intermediate states which would be required for divide-and-conquer. However in differential cryptanalysis we don’t care about the precise value of the internal state as long as a differential relation between inputs propagates throughout the cipher structure far enough to allow us to effectively ‘unroll’ the cipher rounds and thus attack the rounds one by one.

Differential cryptanalysis is usually a chosen plaintext attack (though there are extensions allowing for known plaintext or even ciphertext-only attacks) which uses pairs of plaintext related by a constant difference, usually a XOR operation. The attacker computes the differences of the corresponding ciphertexts and hopes to detect a statistical pattern in their distribution allowing them to distinguish ciphertexts from random. In differential cryptanalysis we will usually target a single component of the wider cipher (eg. an s-box or a round function) where we can reduce the keyspace of a target round key to a size that is bruteforcable. In FEAL-4 for example we are dealing with a 64-bit key which is expanded (using key schedule) into six 32-bit round keys. In the CTF challenge the key scheduling is ommited in favor of directly loading the 6 subkeys into the cipher.

In particular ciphers with an iterated number of individually weak functions (eg. feistel ciphers with a weak round function) are susceptible to differential cryptanalysis. We apply this process for as much rounds as possible to recover as much of the key schedule as possible, filling in any remaining gaps with additional bruteforce, other cryptanalytic attacks or clever heuristics depending on the nature of the cipher. In general we seek to attack r-1 out of r rounds with our analysis. The idea behind differential cryptanalysis is to find a mapping from properties of inputs to properties of outputs and trace this mapping throughout the cipher. Consider block ciphers composed of multiple applications of a round function with each round function combining the intermediate state with the current round key (eg. feistel ciphers). These round functions ought to be non-linear in nature and behave somewhat like Pseudorandom Number Generators (PRNGs) in that we should not be able to predict the output of a round function given its input if we do not know the key. If we can find a property of an input that maps to a certain property in the output with a probability other than what one would expect of a random function (eg. ~0.5**n) this can potentially be exploited to discover information about the key. The way in which properties of inputs map to properties of their corresponding outputs are called characteristics. Consider two inputs x0 and x1 and their ‘input differential’ di = x0 ^ x1. We obtain the output differential as follows:

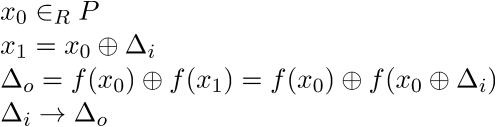
The mapping di -> do is called a differential characteristic. The process of a differential cryptanalytic attack is as follows:

• We choose an appropriate input differential di (determined through analysis of the target function)

• We choose a suitable number of chosen plaintext pairs (p0, p1) related by our input differential, eg. p1 = p0 ^ di, feed them to the cipher and obtain the resultant ciphertext pairs (c0, c1).

• For each ciphertext pair we derive the output differential of as many round functions (or other target functions) as possible in the last round (‘tracing’ the input and output differentials through the cipher’s functions)

• For each possible key value, count the number of pairs that result in the expected output differential using this key value in the last round

• The highest scoring key value is our candidate round key

The ‘tracing’ process, described below, is effectively an extension of the analysis of the round function to the general cipher structure.

Lets clarify some things by example here. Consider FEAL-4’s round function (also called the f-box) and lets say we have plaintexts x0, x1 with input differential d = (x0 ^ x1). Our goal is to predict differentials as far as possible throughout the cipher by injecting these input differentials in the plaintext and monitor how they change as they ‘move’ through the target cipher’s structure. While we cannot know the intermediate output values of the round function (because of application of the unknown round key) this does not affect our differentials as their relationship proceeds through this XOR unaffected since x0 ^ x1 = (x0 ^ k1) ^ (x1 ^ k1). In ‘regular’ FEAL-4 there exists a known input differential 0x80800000 which, when fed into the round function, produces the output differential 0x02000000 with probability 1.0, eg. (fbox(x0) ^ fbox(x0 ^ 0x80800000)) = 0x02000000. Also keep in mind that input differentials of 0x00000000 map to output differentials of 0x00000000 (as identical inputs map to identical outputs). We then call the mappings of input differentials to output differentials 0x80800000 -> 0x02000000, 0x00000000 -> 0x00000000 the differential characteristic for the f-box.

Finding differentials

In order to find a good differential characteristic we need to find one that holds with high probability for any given set of inputs to our target round function. One way to approach this is by running every combination of input pairs through the round function and noting down the occurances of a differential characteristic but this process tends to become infeasible quickly for target functions with larger input sizes. So let’s break things down. Our target round function, f-box, is composed of several applications of g-box. This g-box is a modular addition function followed by some bitshifting which looks as follows (using King’s image of the regular FEAL-4 round function and its g-box here):

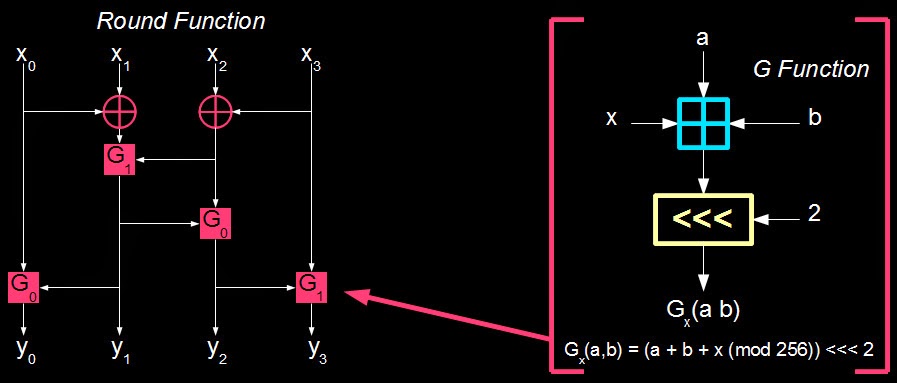
In code:

def rot(x):
  return ((x<<2) | (x>>6)) & 0xff

def g_box(a, b, mode):
  return rot((a + b + mode) & 0xff)

The mode input value is always either 0 or 1 as it distinguishes between two possible g-boxes G0 and G1 and does not affect any differentials because it doesn’t change between plaintext encryptions, so we can treat it as a 0 differential for our purposes. Consider what happens when we feed a 0x80 differential into the g-box without its rotation:

>> a0 = 0xAA
>> b0 = 0x00
>> a1 = a0 ^ 0x80
>> b1 = b0
>> ((a0 + b0) & 0xff) ^ ((a1 + b1) & 0xff))
0x80

Since 0x80 is the most significant bit (10000000b) of a byte this means that if only the MSB changes between two inputs only the MSB will change in the output. This is due to the fact that modular addition relies on carrying to make a bit change affect another bit. When only the MSB changes any carry resulting from the modular addition is dropped and ignored which results in this differential characteristic. This process only works if the input differential to the other input of the modular addition operation (b0 ^ b1 in this case) is 0. After the bit rotation the differential is rotated by 2 which results in 0x02. As such the g-box has the following differential characteristic: 0x80 -> 0x02, 0x00 -> 0x00 (to clarify, this means g_box(a, b, mode) ^ g_box(a ^ 0x80, b ^ 0x00, mode) = 0x0002).

Since our rotation function is different we need to modify this differential. Our FEAL-4 version has the following rotation function:

def rot(x):
  return ((x<<4) | (x>>4)) & 0xff

With this different rotation we get: g_box(a, b, mode) ^ g_box(a ^ 0x80, b ^ 0x00, mode) = 0x0008, ie. differential characteristic 0x80 -> 0x08, 0x00 -> 0x00.

Extending to a full f-box differential

Now we will extend what we know about the g-box to the full FEAL round function (f-box). Consider for a moment regular FEAL-4 again and take a look at the round function as depicted above. Lets consider what happens if we feed it 0x80800000 as input differential. The 32-bit input to the round function is broken up in 4 seperate bytes. The leftmost byte (byte 3) in the above diagram is the MSB of the 32-bit input. We XOR the MSB with byte 2 resulting in an output differential of 0x00 since both input differentials to the XOR operation are identical (0x80). Bytes 0 and 1 are XORed to produce a 0x00 differential as well the input of which is fed to the first g-box resulting in an output differential of 0x00. As the image shows, this process traces the (alternatingly input and output) differentials through the g-box and XOR operations resulting in the following differential characteristics for the FEAL-4 round function: 0x80800000 -> 0x02000000, 0x00000000 --> 0x00000000. The only difference with our version of FEAL-4 is our differential characteristic for g-box so we have the following differential characteristics for f-box: 0x80800000 -> 0x08000000, 0x00000000 --> 0x00000000.

Building the full differential tracing path

Now that we have our differential characteristics for FEAL-4’s round function we will construct the differential characteristic for the full cipher. Chaining differentials together is easier if the input and output differentials are equal but it’s still doable if they are not though some care has to be taken in the process since, as noted in Kerry McKay’s lecture materials we want a high overall probability for multiple rounds, a full characteristic which consists of two individual characteristics one of which has high probability and one of which has low (eg. 0.9*0.1 = 0.09) might be less well-suited than two medium-probability characteristics (eg. 0.5*0.5 = 0.25).

Consider King’s illustration of the full differential tracing path through FEAL-4 below:

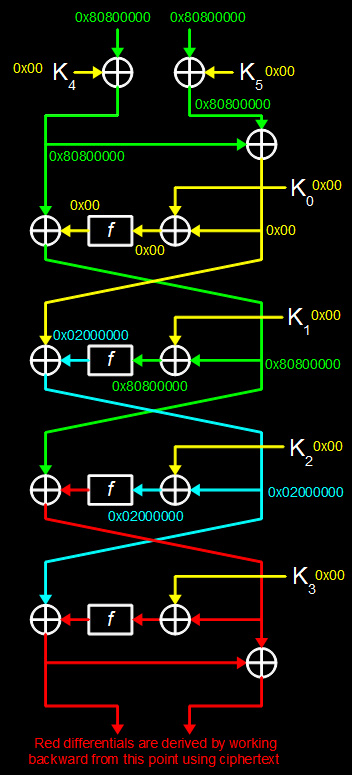
Note that the 0x00 next to the round keys does not denote their value but their differential (as the round keys do not change between plaintext/ciphertext pairs). When a differential hits a round function we cannot predict what the output differential will be except in one of two cases:

• When the input differential is 0: then the output differential is also 0

• When the input differential is our g-box input differential 0x80800000: then the output differential is 0x02000000 for regular FEAL-4 and 0x08000000 for our version.

Consider the input differential 0x8080000080800000 (which is simply the f-box input differential put in the MSBs and LSBs). Its left and right halves get XORed in the first round to become the left half for the next round (becoming 0) and get XORed with the round key before being pulled through the f-box, the output differential of which will be 0 too. This is then XORed against the left half of the input and becomes the right half for the next round. In the subsequent round we have the input differential 0x0000000080800000 (because the left half became 0 in the previous round) which results in a right-half differential of 0x02000000 for regular FEAL-4 and 0x08000000 for our version. The left half is lost here as we don’t know the output differential corresponding to either 0x02000000 or 0x08000000 as an input differential for the f-box.

So now we need to figure out what the output differential for the 3rd round is. We want to know the output differential of the final f-box application and we know that it was XORed with right-hand differential of the previous round to produce the left-half of the ciphertext. Hence given two chosen plaintext/ciphertext pairs (where (p0, c0), (p1, c1) and p0 ^ p1 = input_differential) we XOR the 4 most significant bytes of c0 with those of c1 obtaining x. We then XOR x with 0x02000000 (or 0x08000000 in our case) to find the last round function’s output differential.

For the first 3 rounds we have input differentials (0x8080000080800000, 0x0000000080800000, 0x0000000002000000 in the example) and a single output differential 0x02000000. In our FEAL-4 version these will be:

input_diff_1 = 0x8080000080800000
input_diff_2 = 0x0000000080800000
input_diff_3 = 0x0000000008000000
output_diff = 0x0000000008000000

Finding the round keys

We will proceed as follows:

• First we crack the subkey of final round 4: subkey[3]

• Then we will crack the subkeys of rounds 3 and 2: subkey[1], subkey[2]

• Finally we will crack the subkey of round 1: subkey[0] and the subkeys used for initialization: subkey[4], subkey[5]

But what do we do with all this information about differentials? How does this allow us to obtain a round key? Intuitively: we know that a differential characteristic has an exact probability so given a series of inputs x and corresponding outputs y generated by key candidate k the candidate that matches the differential characteristic with closest to the expected probability is our most likely candidate key, ie. we use our plaintext/ciphertext pairs to see if what the candidate key produces matches with our collected pairs and the known characteristic of the cipher.

In order to understand a bit better how the differentials can help us recover a subkey faster than bruteforce consider the following toy scenario: we have two inputs x0 and x1 related by input differential di = x0 ^ x1 and their outputs y0 and y1 where yi = sbox(xi) and the outputs are related by output differential do = y0 ^ y1. Consider the following 4-bit sbox given as an example by Jon King:

A good differential characteristic of the above s-box is 4 -> 7 (since there are 6 out of 16 values for which this holds, eg. (5 ^ 1) = 4 -> (9 ^ 14) = 7). Now we target a simple cipher using this sbox as a round function and use it to illustrate our approach for attacking a round:

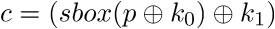
We know plaintexts (1, 5) and ciphertexts (0, 7) so we can confirm whether subkey guesses k0, k1 hold by matching them against the corresponding s-box inputs and outputs since plaintext ^ s_box_input = k0 and ciphertext ^ s_box_output = k1. Eg. if we guess k0 = 9 that would make the s-box inputs (8, 12) and outputs (8, 13) and hence the output differential 8 ^ k1 ^ 13 ^ k1 = 5 which doesn’t match our differential characteristic so we discard this guess. If we guess k0 = 8 however we get s-box mapping (9,13) -> (11, 12) with output differential 11 ^ 12 = 7 which does match our differential characteristic so we increment the score of candidate round key k0 = 8 until we have a candidate for which the score is equal to the number of chosen plaintext/ciphertext pairs (ie. matches all of them). If we do, we add this candidate to the valid candidate list (since multiple candidates might validate). This last part is where we diverge from King (as did h4x0rpsch0rr) as his approach is prone to false positives from which the algorithm cannot recover (since it simply goes with the first validating candidate and moves on to the next round keys). Cracking a 32-bit round key looks as follows in pseudo-code:

valid_candidates = []
for keyguess in xrange(0, 2**32):
  score[keyguess] = 0
  for j in number_of_plaintext_pairs:
    round_input_guess_0 = (round_plaintext_0[j] ^ keyguess)
    round_input_guess_1 = (round_plaintext_1[j] ^ keyguess)

    round_output_guess_0 = sbox(round_input_guess_0)
    round_output_guess_1 = sbox(round_input_guess_1)

    if ((round_output_guess_0 ^ round_output_guess_1) == output_differential):
      score[keyguess]++

  if (score[keyguess] == number_of_plaintext_pairs):
    valid_candidates.append(keyguess)

Do note that the success rate here depends on the number of chosen plaintext/ciphertext pairs. The more pairs we test against the slower the attack but the higher the confidence we have in the round keys (and the less chance of false positives). It might be a little counter-intuitive that using a differential characteristic with a higher probability (such as our FEAL-4 characteristic with probability 1.0) means we have to make more key guesses (since there are more input/output pairs related by the differential) but it also means it is easier to find a usable pair since a pair that doesn’t match the differential characteristic cannot be used in the attack (since the characteristic is used to confirm a keyguess).

We will start by cracking the subkey of the last round. We want to recover the inputs and outputs to the last round function f-box from the ciphertext. Take a look at the last round:

cipherLeft = list_xor(R4L, f_box(list_xor(R4R, self.subkeys[3])))
cipherRight = list_xor(cipherLeft, R4R)

We can obtain R4R = cipherLeft ^ cipherRight which gives us the input to the f-box (before the round key is mixed in). The output of the f-box is cipherLeft ^ R4L. We do not have R4L but we do know its differential is 0x0000000008000000 (since it is the output of the previous round) so we can calculate the output differential of f-box as the XOR between the differential of R4L (traced through the cipher) and cipherLeft. Now that we have our f-box candidate input we can evaluate it using f-box and see if it matches the expected output differential in the manner described above to test the round key.

Once we have subkey 3 we can undo the last round of the cipher and start attacking subkey 2, repeating this process throughout the rest of the rounds. A catch here is that we can’t use the same differential path here for these rounds so instead we will have to build a shortened differential path with another differential characteristic which is traced through the cipher up until before the round we are targeting. This is where the earlier described input differentials come in:

input_diff_1 = 0x8080000080800000
input_diff_2 = 0x0000000080800000
input_diff_3 = 0x0000000008000000

The first differential traces up to before round 4, the second one up to before round 3 and the final one up to before round 2. So we will need 3 sets of n chosen plaintext/ciphertext pairs each, with plaintext pairs generated according to the above differentials. The full process for cracking the cipher then becomes (working backwards from round 4):

input_differentials = [0x8080000080800000, 0x0000000080800000, 0x0000000008000000]
output_differential = 0x0000000008000000

for i in [3..1]
  pairs = collect_chosen_pairs(N, input_differentials[0])
  undo_final_operation(pairs) # undo final feistel operation
  for j in [0..(3-i)]:
    undo_last_round(subkey[3-j])
  crack_round_key(pairs, output_differential)

Note that the above code assumes we retrieve only 1 candidate round key. In practice we will retrieve a set of candidate round keys only 1 of which is correct. Thus it might occur we work our way to the next round key using a false round key and we will have to revert. I wrote a backtracking-based approach capable of dealing with false positives to address this.

Once we complete this process we have subkeys 1 to 3 and we move on to the first round to obtain subkey 0. We can’t use differentials here to test its subkey and in addition there are the two initialization subkeys (4 and 5). We will recover all three in one cracking attempt by guessing a candidate subkey[0] and decrypting the first round (using the material obtained from decrypting the other rounds with our recovered subkeys). We then use our chosen plaintext pair to determine the subkey[4] and subkey[5] corresponding to this candidate subkey[0]. The subkey[0] candidate which keeps the corresponding subkey[4] and subkey[5] consistent among all chosen-plaintext pairs is the correct subkey[0] which gives us both a way to validate subkey[0] guess and recover the initialization subkeys in one go. Again, here too we have to take false positive keys into account. In pseudocode this looks as follows:

k0_candidates = []
k4_candidates = []
k5_candidates = []

for k0_guess in xrange(0, 2**32):
  k4_guess, k5_guess = 0
  for j in number_of_plaintext_pairs:
    plain_left0 = left_half(round_plaintext_0[j])
    plain_right0 = right_half(round_plaintext_0[j])

    cipher_left0 = left_half(intermediate_ciphertext[j])
    cipher_right0 = right_half(intermediate_ciphertext[j])

    y = f_box(cipher_right0 ^ k0_guess) ^ cipher_left0

    # Make first guess attempt
    if not yet guessed k4:
      k4_guess = y ^ plain_left0
      k5_guess = y ^ cipher_right0 ^ plain_right0
    # Maintain consistency
    else if ((y ^ plain_left0 != k4_guess) or (y ^ cipher_right0 ^ plain_right0 != k5_guess)):
      k4_guess = incorrect
      k5_guess = incorrect
      break

  if (k4_guess != incorrect):
    k0_candidates.append(k0_guess)
    k4_candidates.append(k4_guess)
    k5_candidates.append(k5_guess)

After this process has completed we have recovered a set of candidate key schedules each of which we will test against a seperate chosen plaintext/ciphertext pair for final validation.

Collecting our chosen plaintext-ciphertext pairs

In order to obtain the chosen plaintext material for our attack we should query the server encryption oracle, generating three seperate sets of 6 chosen plaintext pairs (12 chosen plaintexts in total) each where each pair was related by one of the three input differentials. We then extract the relevant FEAL-4 plaintext/ciphertext blocks from these pairs by using the method described above for chopping up the block cipher mode of operation. Once we have our chosen plaintext-ciphertext materials we can feed them into the differential cryptanalysis code. Unfortunately the server hosting the challenge was already down by the time i started working on this so instead i simply modified the server code to use custom round keys (and removed the time-consuming proof-of-work check).

Speeding up the attack

The code accompanying this article is highly unoptimized (for one, it’s written in Python) since it serves as an illustration but the above attack can be sped up not only by porting it to eg. C but by parallelizing the attack where possible. Both the cracking of an individual round key and the backtracking process can be parallelized by breaking up the search space for each round key into N segments, assigning each segment to a different core or CPU. Each segment would contain (starting from the ‘top’ round) every candidate subkey in the range [(2**32 / N)*i, (2**32 / N)*(i+1)] and all potential paths growing down (several) rounds from there.

Finalizing the attack

So, to summarize, we:

• Chop up the mode of operation to extract FEAL-4 plaintext/ciphertext pairs

• Adapt the differential characteristic to our modified FEAL-4 version

• Use the encryption oracle for adaptive chosen plaintext collection

• Feed all this into our FEAL-4 differential cryptanalysis code:

# Round key cracking function
def crack_round_key(pairs, output_differential):
    valid_candidates = []
    candidate_key = 0
    while (candidate_key < 2**32):
        score = 0
        for i in xrange(len(pairs)):
            cipher_left = left_half(pairs[i][0][1])
            cipher_left ^= left_half(pairs[i][1][1])
            cipher_right = right_half(pairs[i][0][1])
            cipher_right ^= right_half(pairs[i][1][1])

            y = cipher_right
            z = (cipher_left ^ output_differential)

            candidate_right = right_half(pairs[i][0][1])
            candidate_left = left_half(pairs[i][0][1])
            candidate_right2 = right_half(pairs[i][1][1])
            candidate_left2 = left_half(pairs[i][1][1])

            y0 = candidate_right
            y1 = candidate_right2

            candidate_input0 = y0 ^ candidate_key
            candidate_input1 = y1 ^ candidate_key
            candidate_output0 = f_box(candidate_input0)
            candidate_output1 = f_box(candidate_input1)
            candidate_differential = (candidate_output0 ^ candidate_output1)

            if (candidate_differential == z):
                score += 1
            else:
                break

        if (score == len(pairs)):
            valid_candidates.append(candidate_key)

        candidate_key += 1

    return valid_candidates

# Undo last FEAL-4 round
def undo_last_round(pairs, round_key):
    for i in xrange(len(pairs)):
        cipher_left0 = left_half(pairs[i][0][1])
        cipher_right0 = right_half(pairs[i][0][1])

        cipher_left1 = left_half(pairs[i][1][1])
        cipher_right1 = right_half(pairs[i][1][1])

        cipher_left0 = cipher_right0
        cipher_left1 = cipher_right1
        cipher_right0 = f_box(cipher_left0 ^ round_key) ^ (pairs[i][0][1] >> 32)
        cipher_right1 = f_box(cipher_left1 ^ round_key) ^ (pairs[i][1][1] >> 32)

        pairs[i][0][1] = combine_halves(cipher_left0, cipher_right0)
        pairs[i][1][1] = combine_halves(cipher_left1, cipher_right1)

    return pairs

# Undo final operation of a Feistel round (cipherLeft ^ R4R)
def undo_final_operation(pairs):
    for i in xrange(len(pairs)):
        cipher_left0 = left_half(pairs[i][0][1])
        cipher_right0 = right_half(pairs[i][0][1]) ^ cipher_left0

        cipher_left1 = left_half(pairs[i][1][1])
        cipher_right1 = right_half(pairs[i][1][1]) ^ cipher_left1

        pairs[i][0][1] = combine_halves(cipher_left0, cipher_right0)
        pairs[i][1][1] = combine_halves(cipher_left1, cipher_right1)

    return pairs

# Backtracking approach to cracking rounds 2 to 4 (subkeys 2, 3 and 4)
def phase1(current_round, subkeys = [], output_differential = 0, chosen_pairs = []):
    valid_candidates = []
    # Work our way back from final round 4 (index 3) to round 2 (index 1)
    if (current_round == 0):
        # If we get to this point in a path, we recovered a candidate partial key schedule that's valid from rounds 4 to 2
        return [subkeys[::-1]]
    else:
        print "[*] Cracking round %d, using output differential %lx ..." % (current_round+1, output_differential)
        # Take chosen plaintext pairs crafted with input differential tailored to this round, undo final Feistel operation

        pairs = undo_final_operation(chosen_pairs[current_round])
        # Undo previous rounds with round keys extracted so far in this path
        for j in xrange(0, (3-current_round)):
            pairs = undo_last_round(pairs, subkeys[j])

        # Obtain candidates for this round
        candidate_roundkeys = crack_round_key(pairs, output_differential)
        
        if (len(candidate_roundkeys) == 0):
            # Failed to find any subkey candidates for this round using given recovered keyschedule, backtrack...
            return []
        else:
            for candidate_k in candidate_roundkeys:
                print "[*] Trying candidate subkey [0x%08x] for round %d ..." % (candidate_k, current_round+1)
                r = phase1(current_round-1, subkeys + [candidate_k], output_differential, chosen_pairs)
                if (len(r) > 0):
                    # We've recovered a valid partial key schedule
                    valid_candidates += r

    return valid_candidates

# Crack round 1 and subkeys 1, 5 and 6
def phase2(candidate_schedules = [], chosen_pairs = [], multi = False):
    valid_schedules = []
    for subkeys in candidate_schedules:
        # Take pairs for round 2, strip to round 1
        pairs = undo_last_round(chosen_pairs[1], subkeys[0])

        k0_guess = 0
        while (k0_guess < 2**32):
            k4_guess = None
            k5_guess = None

            for j in xrange(len(pairs)):
                plain_left0 = left_half(pairs[j][0][0])
                plain_right0 = right_half(pairs[j][0][0])

                cipher_left0 = left_half(pairs[j][0][1])
                cipher_right0 = right_half(pairs[j][0][1])

                y = (f_box(cipher_right0 ^ k0_guess) ^ cipher_left0)

                # Make first guess attempt
                if (k4_guess == None):
                    k4_guess = (y ^ plain_left0)
                    k5_guess = (y ^ cipher_right0 ^ plain_right0)
                
                # Maintain consistency across pairs
                elif ((y ^ plain_left0 != k4_guess) or (y ^ cipher_right0 ^ plain_right0 != k5_guess)):
                    k4_guess = None
                    k5_guess = None
                    break

            # Valid k0, k4, k5 combo found, adjust key schedule
            if ((k4_guess != None) and (k5_guess != None)):
                subkeys.insert(0, k0_guess)
                subkeys.insert(4, k4_guess)
                subkeys.insert(5, k5_guess)
                break

            k0_guess += 1

        # If we've recored a valid full key schedule we immediately return it if we don't require multiple possible valid key schedules, else we add it to a list
        if(len(subkeys) == 6):
            if (multi):
                valid_schedules.append(subkeys)
            else:
                return [subkeys]

    return valid_schedules

# Combine backtracking routines into single complete differential cryptanalysis routine
def differential_cryptanalysis(output_differential, chosen_pairs):
    subkeys = []

    # Crack final 3 round keys
    candidate_schedules = phase1(3, subkeys, output_differential, chosen_pairs)

    if (len(candidate_schedules) == 0):
        print "[-] Failed to crack round keys 2 to 4..."
        return
    else:
        print "[*] Recovered %d candidate partial key schedules..." % len(candidate_schedules)

    # Crack first 3 round keys
    return phase2(candidate_schedules, chosen_pairs, False)

And that’s it, one block cipher down, one to.

Attacking the second block cipher: Meet-in-the-Middle Attack against a Lai-Massey scheme

Our next step is to break the second block cipher which is part of our target scheme. Remember that since we have broken the first block cipher (FEAL-4) we effectively have a chosen plaintext scenario for tackling this cipher as well should we need it. Lets look at its code:

  def split_int(m):
      return ((m>>16) & 0xFFFF, m & 0xFFFF)

  def join_int(l, r):
      return (l<<16) | r

  def orth(m):
      (l, r) = split_int(m)
      return join_int(r, l ^ r)

  def inv_orth(m):
      (l, r) = split_int(m)
      return join_int(l ^ r, l)

  def F(m, subkey):
      (l, r) = split_int(m)
      (k_l, k_r) = split_int(subkey)
      (mul_l, mul_r) = split_int(l * r)
      l = ((mul_l + r) * k_l) & 0xFFFFFFFF
      r = ((mul_r * l) + k_r) & 0xFFFFFFFF
      l = ((l<<7) | (l>>25)) & 0xFFFFFFFF
      r = ((r<<18) | (r>>14)) & 0xFFFFFFFF
      return r ^ l


  def M(L, R, subkey):
      A = F((L - R) & 0xFFFFFFFF, subkey)
      CL = orth((L + A) & 0xFFFFFFFF)
      CR = (R + A) & 0xFFFFFFFF
      return (CL, CR)

  def inv_M(L, R, subkey):
      L = inv_orth(L)
      A = F((L - R) & 0xFFFFFFFF, subkey)
      PL = (L - A) & 0xFFFFFFFF
      PR = (R - A) & 0xFFFFFFFF
      return (PL, PR)


  class bc2(object):

      def __init__(self, key):
          (k0, k1, k2, k3) = struct.unpack('>HHHH', key)
          K0 = pow(k0, 2)
          K1 = pow(k1, 2)
          K2 = pow(k2, 2)
          K3 = pow(k2, 2)
          self.subkeys = [K0, K1, K2, K3]

      def encrypt_block(self, plaintext):
          (L0, R0) = struct.unpack('>II', plaintext)
          (L1, R1) = M(L0, R0, self.subkeys[0])
          (L2, R2) = M(L1, R1, self.subkeys[1])
          (L3, R3) = M(L2, R2, self.subkeys[2])
          (CL, CR) = M(L3, R3, self.subkeys[3])
          return struct.pack('>II', CL, CR)

      def decrypt_block(self, ciphertext):
          (L0, R0) = struct.unpack('>II', ciphertext)
          (L1, R1) = inv_M(L0, R0, self.subkeys[3])
          (L2, R2) = inv_M(L1, R1, self.subkeys[2])
          (L3, R3) = inv_M(L2, R2, self.subkeys[1])
          (PL, PR) = inv_M(L3, R3, self.subkeys[0])
          return struct.pack('>II', PL, PR)

The above cipher consists of 4 rounds and uses 4 subkeys of 16 bits each (having a total key schedule size of 64 bits). Its structure is a Lai-Massey scheme (used in eg. IDEA) whose rounds look as follows: (L1, R1) = M(L0, R0, K0) = (orth((L + A)), (R + A)) where A = F(L - R, K0). Note that all addition and subtraction here is modular. The orth function applied to the left half is an ‘almost’ orthomorphism commonly used in Lai-Massey schemes intended to prevent a trivial distinguishing attack via L0 - R0 = Ln+1 - Rn+1. Also note that the round function F does not have to be invertible.

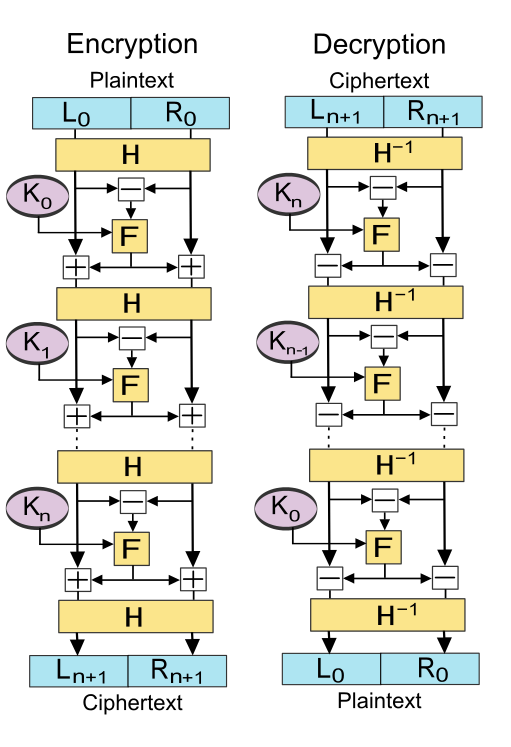
Considering the hint Are the rounds of the second block cipher completely dependent or independent of each other? Or is the truth somewhere in the middle? we suspect a Meet-in-the-Middle (MitM) attack.

Meet-in-the-Middle Basics

A MitM attack is a time/space tradeoff attack which targets ciphers composed of a series of invertible functions. It is a known plaintext attack which requires the possesion of a set of plaintexts and their corresponding ciphertexts. Essentially, it is a divide-and-conquer approach which splits the cipher into seperate parts and determines the intersections of their intermediate states, working forward from the plaintext and backward (through the inverse of the target function) from the ciphertext. A trivial example would be 2-DES which is simply c = DES_ENCRYPT(DES_ENCRYPT(p, k0), k1) where one could be led to believe the double application of DES with two n-bit keys presents a 2^(2*n) attack complexity. However using a Meet-in-the-Middle attack one can reduce the complexity to 2^n + 2^n = 2^(n+1) as follows:

for k0_candidate in xrange(2**n):
    ci = DES_ENCRYPT(k0_candidate, p)
    lookup_table[ci] = k0_candidate

for k1_candidate in xrange(2**n):
    ci = DES_DECRYPT(k1_candidate, c)
    if (ci in lookup_table):
        candidates.add((lookup_table[ci], k1_candidate))

This concept applies equally whether we are dealing with 2 applications of a full block cipher or simply a block cipher with 2 rounds. The principle is illustrated in this image by agilebits:

The principle also extends to multiple rounds, called a multi-dimensional MitM. This does, however, involve additional computation since we will have to guess intermediate states we cannot reach from the plaintext or ciphertext. Depending on the intermediate state size (possibly a whole block) this doesn’t seem like an attractive path to go down. The alternative seems to be meeting all combinations between k0,k1 with all combinations of k2,k3 which would be of complexity 2**32 + 2**32 = 2**33, feasible but with a large lookup table (2**32 * 8B = 32GB). Not attractive either.

The MitM attack on BC2

Luckily, however, we can spot a typo in the bc2 implementation which allows us to perform a normal 1-dimensional MitM with a 2**16 * 8B = 512KB lookup table:

         (k0, k1, k2, k3) = struct.unpack('>HHHH', key)
          K0 = pow(k0, 2)
          K1 = pow(k1, 2)
          K2 = pow(k2, 2)
          K3 = pow(k2, 2)
          self.subkeys = [K0, K1, K2, K3]

As we can see K3 = K2 = pow(k2, 2) here due to a typo which means that we can unroll the last two rounds with one candidate key guess which makes the attack complexity feasible enough for a CTF problem. Our approach is as follows (keep in mind bc2 is used in decryption mode in the overall cipher so encryption/decryption and plaintext/ciphertext here are swapped from the regular scenario):

• We gather a two plaintext/ciphertext pairs, one for the attack and one for confirmation

• For all (2**16) possible subkeys k3 we peform inverse round function inv_M on the ciphertext twice (using k3 as k2 the second time) and store the result in a lookup table associating it with k3

• For all (2**32) possible combinations of k0 and k1 we apply M twice to the plaintext (first with k0 then with k1) and check whether the intermediate state is in the lookup table. If so we validate the corresponding round keys against the confirmation pair and if this validates as well we quit, having found our key schedule.

While the validation isn’t required per se it could be possible (depending on the function we are attacking) that we find enc(p, x) = dec(c, y) for (x,y) such that enc(enc(p, x), y) != c, ie. we find a false keypair that is particular to a single plaintext/ciphertext pair but is not the actual keypair.

Speeding up the attack

This attack can be sped regarding three aspects, the first of which is in the construction of the lookup table which is a parallelizable task (one can segment the k3 keyspace into N segments each of which are handled by a seperate core/CPU) and the second of which consists of creating a more appropriate hashtable for lookups rather than the Python one which i used in my example. Finally the lookup operation itself is parallelizable as well as the keyspace of k0 and k1 can be segmented.

Finalizing the attack

I wrote the following script to carry out the above MitM attack:

def compute_lookup_table(target_ciphertext):
    lookup_table = {}
    for k3_candidate in xrange(2**16):
        (L0, R0) = struct.unpack('>II', target_ciphertext)
        (L1, R1) = inv_M(L0, R0, k3_candidate)
        (L2, R2) = inv_M(L1, R1, k3_candidate)
        lookup_table[(L2, R2)] = k3_candidate
    return lookup_table

def brute_force_lookup(lookup_table, target_plaintext, confirmation_plaintext, confirmation_ciphertext):
    for k0_candidate in xrange(2**16):
        for k1_candidate in xrange(2**16):
            (L0, R0) = struct.unpack('>II', target_plaintext)
            (L1, R1) = M(L0, R0, k0_candidate)
            (L2, R2) = M(L1, R1, k1_candidate)

            if ((L2, R2) in lookup_table):
                candidate_subkeys = [k0_candidate, k1_candidate, lookup_table[(L2, R2)], lookup_table[(L2, R2)]]
                if (encrypt_block(confirmation_plaintext, candidate_subkeys) == confirmation_ciphertext):
                    return candidate_subkeys
    return None

def perform_mitm(target_plaintext, target_ciphertext, confirmation_plaintext, confirmation_ciphertext):
    print "[*] Building lookup table ..."
    lookup_table = compute_lookup_table(target_ciphertext)  
    print "[*] Finished building lookup table, performing lookup ..."
    subkeys = brute_force_lookup(lookup_table, target_plaintext, confirmation_plaintext, confirmation_ciphertext)
    # Undo the pow(round_key, 2) operation in key scheduling
    return [sqrt(x) for x in subkeys]

Combining both attacks to solve the challenge

We can combine the above attacks on the seperate block ciphers to crack to overall cipher protecting the flag using this script:

from feal4_differential_cryptanalysis import *
from bc2_mitm_attack import *

output_differential = 0x0000000008000000

print "[*] Collecting chosen plaintexts ..."

pairs_2 = bc1_chosen_plaintexts(12, 0x0000000008000000)
pairs_3 = bc1_chosen_plaintexts(12, 0x0000000080800000)
pairs_4 = bc1_chosen_plaintexts(12, 0x8080000080800000)

print "[*] Mounting differential cryptanalysis attack ..."

valid_schedules = differential_cryptanalysis(output_differential, [None, pairs_2, pairs_3, pairs_4])

assert (len(valid_schedules) == 1)
subkeys_bc1 = valid_schedules[0]

print "[*] Collecting known plaintexts ..."

plaintext0, ciphertext0 = get_bc1_bc2_ciphertext(qword_to_bytes(0x0BADC0DEF00DFACE))
plaintext1, ciphertext1 = get_bc1_bc2_ciphertext(qword_to_bytes(0xC0DEFACE0BADF00D))

print "[*] Mounting MitM cryptanalysis attack ..."

subkeys_bc2 = perform_mitm(ciphertext0, plaintext0, ciphertext1, plaintext1)

assert (subkeys_bc2 != None)

print "[+] Recovered valid BC_1 key schedule [0x%08X, 0x%08X, 0x%08X, 0x%08X, 0x%08X, 0x%08X]!" % (subkeys_bc1[0], subkeys_bc1[1], subkeys_bc1[2], subkeys_bc1[3], subkeys_bc1[4], subkeys_bc1[5])
print "[+] Recovered valid BC_2 key schedule: [0x%04X, 0x%04X, 0x%04X, 0x%04X]!" % (subkeys_bc2[0], subkeys_bc2[1], subkeys_bc2[2], subkeys_bc2[3])

Running the above attack against the challenge server will (after some time) recover the seperate key schedules which we can then use to decrypt any ciphertext originating from the server (including the flag):

$ python five_blocks_attack.py 
[*] Collecting chosen plaintexts ...
[*] Mounting differential cryptanalysis attack ...
[*] Cracking round 4, using output differential 8000000 ...
[*] Trying candidate subkey [0x00000004] for round 4 ...
[*] Cracking round 3, using output differential 8000000 ...
[*] Trying candidate subkey [0x00000003] for round 3 ...
[*] Cracking round 2, using output differential 8000000 ...
[*] Trying candidate subkey [0x00000002] for round 2 ...
[*] Recovered 1 candidate partial key schedules...
[*] Collecting known plaintexts ...
[*] Mounting MitM cryptanalysis attack ...
[*] Building lookup table ...
[*] Finished building lookup table, performing lookup ...
[+] Recovered valid BC_1 key schedule [0x00000001, 0x00000002, 0x00000003, 0x00000004, 0x00000005, 0x00000006]!
[+] Recovered valid BC_2 key schedule: [0x0007, 0x0008, 0x0009, 0x0009]!

Conclusion

Using the two retrieved key schedules we can apply them to decrypt the flag. As i said above the challenge server was down by the time i started looking at this stuff but as the h4x0rpsch0rr writeup reports the combined keyschedules turned out to be 6c 21 3c 29 7b 03 fd 17 cb e3 b8 c8 bb d7 f1 03 d2 2a 2c 0e cc f5 48 dd e9 6a 5d 75 63 1e cc cc and the flag turned out to be VolgaCTF{FEAL_is_weak_the_other_is_MITMable_and_the_mode_is_splittable}.

Either way, the challenge serves as a good, practical introduction to two valuable cryptanalytic techniques which are a good addition to the toolbox of anyone interested in (offensive) security in general and cryptography in particular. As said in the intro while this isn’t going to help you break a solid modern cipher, there’s still a lot of proprietary stuff out there waiting to be broken.